Constructions de base
Constructions à la règle et au compas
En géométrie, la règle (non graduée) et le compas sont les outils de base permettant de travailler en géométrie plane.
Médiatrice d'un segment
La principale construction de la géométrie est sans doute le tracé de la médiatrice d'un segment.
Définition
La médiatrice du segment est la droite qui coupe perpendiculairement le segment en son milieu. Mais c'est aussi l'ensemble des points équidistants des extrémités du segment.
Construction
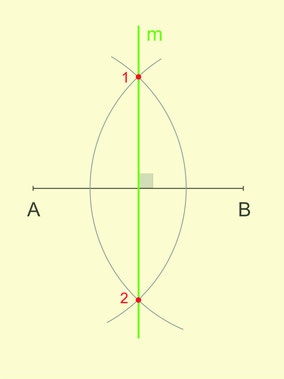
- Pour tracer la médiatrice d'un segment on trace deux arcs de cercle de même rayon de centre A et B respectivement.
- Ces deux arcs se coupent en deux points situés à égale distance des extremités du segment.
- La droite qui passe par les points 1 et 2 est la médiatrice du segment.
Bissectrice d'un angle
Définition
La bissectrice est la demi-droite qui partage l'angle en deux parties égales. C'est à dire, l'axe de symétrie de l'angle.
Construction
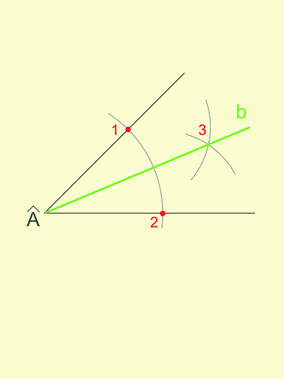
- Pour tracer la bissectrice de l’angle, on trace un arc de cercle de centre A qui coupe les deux côtés de l'angle en A et B respectivement.
- Puis on trace deux arcs de cercle de même rayon, l’un de centre A, l’autre de centre B.
- Ces deux arcs de cercle se coupent en un point 3 équidistant des deux côtés de l'angle.
- La demi-droite partant de A et qui passe par 3 est la bissectrice de l'angle Â.
Construction de l'angle de 60º au compas
Le rapporteur
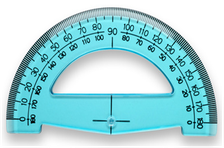
Le rapporteur est l'instrument de mesure qu'on emploie en géométrie pour déterminer la mesure d'un angle. Il existe différents types de rapporteurs. Celui scolaire est un demi-cercle, souvent en plastique et gradué en degrés (de 0º à 180º).
Ici une animation pour vous entraîner à utiliser le rapporteur : "Le permis rapporteur"
Il y a une méthode pour construire un angle de 60º sans rapporteur, mais à l'aide de la règle et du compas. C'est une construction de base qui nous permettra de construire d'autres angles de mesures variées.
Construction
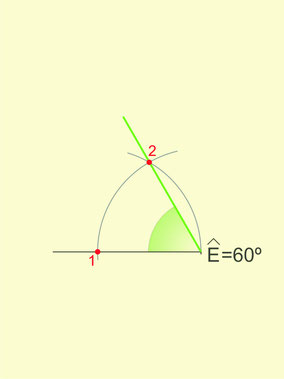
- On trace une demi-droite d'origine E.
- On trace un arc de cercle de centre E qui coupe la demi-droite dans le point 1.
- Avec le même rayon on trace un autre arc de cercle qui coupe celui traçé en 2.
- La demi-droite partant de E et qui passe par le point 2 est l'autre côté d'un angle qui mesure 60º.
Perpendiculaire à une demi-droite par son extremité
Construction
Cette construction est basée sur celle de l'angle de 60º nous permettant de construire un angle droit (90º).
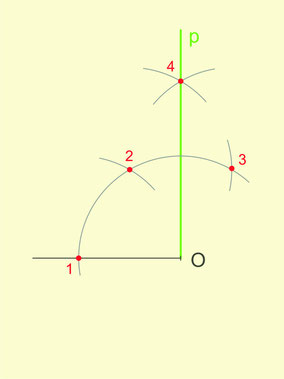
- On pointe le compas sur le point O, extremité de la demi-droite et on trace un arc de cercle.
- Depuis l'intersection de cet arc avec la demi-droite (point 1) on trace un autre arc de même rayon traçant le point 2 et encore une fois pour le point 3.
- Finalement, on trace deux arcs de même rayon, l'un de centre 1 et l'autre de centre 3. Ces deux arcs se coupent en un point 4.
- La demi-droite d'origine O et passant par 4 est la perpendiculaire cherchée.
Division d'un segment en n parties égales (Théorème de Thalès)
C'est qui Thales?
Thalès de Milet est un philosophe et mathématicien grec du VI siècle avant JC. Il est un des sept sages de la Grèce antique. Il est connue par ses découvertes dans le domain de la géométrie. Il nous a laisé le théorème dit "théorème de Thalès" qui est étudié par des élèves dans le monde entier.

Le thèorème de Thalès sert à diviser un segment en parties égales.
Pour expliquer cette construction on va substituer la lettre "n" par le numéro "5". C'est à dire, on va diviser el segment en 5 parties égales.
Construction
- On trace une demi-droite quelconque d'origine A.
- On trace un arc de cercle de centre A et un rayon quelconque. Cet arc coupe la demi-droite en 1.
- En reportant la même longueur avec le compas, on obtient les points suivants: 2, 3, 4 et 5.
- On trace le segment reliant les points 5 et B.
- On trace des paralèlles au segment 5B par les points 4, 3, 2 et 1. Cettes paralèlles partagent le segment AB en cinq parties égales.
Perpendiculaire à une droite par un point extérieur
Construction
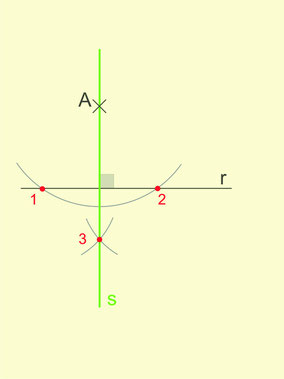
- On trace un arc de cercle de centre A qui coupe la droite r en deux points, les points 1 et 2.
- Ensuite, on trace deux arcs de même rayon de centres 1 et 2 respectivement.
- Ces deux arcs se coupent en 3.
- Il ne reste que tracer la droite qui passe par le point donné A et le point 3.
Perpendiculaire à une droite par un point de la droite
Construction
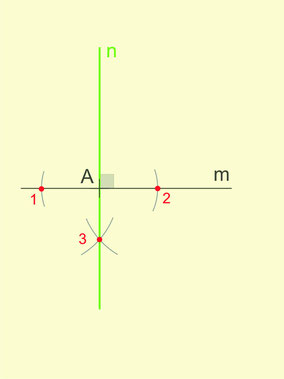
- On trace un arc de cercle de centre A qui coupe la droite m en deux points, les points 1 et 2.
- Ensuite, on trace deux arcs de même rayon de centres 1 et 2 respectivement.
- Ces deux arcs se coupent en 3.
- Il ne reste que tracer la droite qui passe par le point donné A et le point 3.
Parallèle à une droite par un point extérieur
Construction
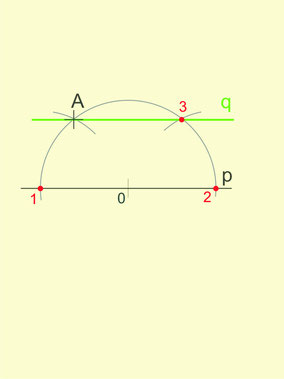
- D'abord, on choisis un point sur la droite comme centre d'un arc de cercle qui passe par le point donné A. Cet arc coupe la droite aux points 1 et 2.
- Avec la compas on prend l'écartement entre les points 1 et A et on le reporte de l'autre côté de l'arc en traçant le point 3.
- La droite paralèlle cherchée passe par A et par 3.