Triangles
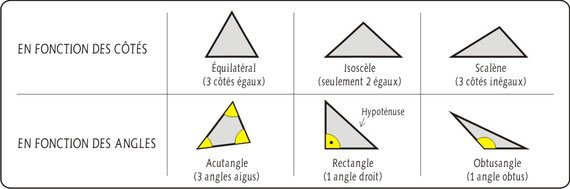
Classement des triangles
Droites et points remarquables
1. Les médiatrices et le centre du cercle circonscrit
La médiatrice d'un segment est la droite perpendiculaire à ce segment en son milieu. Les médiatrices dans un triangle sont donc les médiatrices des côtés de ce triangle. Dans un triangle, les médiatrices sont concourantes, c'est-à-dire qu'elles se coupent en un point. Ce point est le centre du cercle circonscrit au triangle. Le cercle circonscrit est le cercle qui passe par tous les sommets du triangle.
Construction du cercle circonscrit (Shockwave Flash)
2. Les médianes et le centre de gravité
Dans un triangle, une médiane est une droite qui passe par un sommet et le milieu du côté opposé. Les médianes sont concourantes en un point appelé centre de gravité du triangle (isobarycentre).
3. Les hauteurs et l'ortocentre.
Dans un triangle, une hauteur est une droite passant par un sommet et perpendiculaire au côté opposé. Les trois hauteurs sont concourantes en un point appelé ortocentre du triangle.
4. Les bissectrices et le centre du cercle inscrit.
La bissectrice d'un angle est la droite qui partage cet angle en deux angles de même mesure. C'est également l'axe de symétrie de cet angle. Les trois bissectrices d'un triangle sont concourantes en un point appelé centre du cercle inscrit au triangle. Le cercle inscrit est le cercle tangent aux 3 côtés du triangle.
Droite d'Euler
Le mathématicien suisse du XVIIIe siècle Leonhard Euler a découvert que pour n'importe quel triangle l'ortocentre, le centre de gravité et le centre du cercle circonscrit au triangle sont sur une même droite. C'est pour cela que cette droite est appelée droite d'Euler.